MokaByte Numero 10 - Luglio 1997


 

Grafica vettoriale con Java VII
 Archi ancora tesi! 

 

di  

Domenico De Riso
 VII parte
 

 
 

La trattazione degli archi continua perchè leggermente complicata.
La difficoltà maggiore sta nel fatto che gli archi sono curvi e quando vengono manipolati con la Geometria analitica necessitano di equazioni di secondo grado per essere rappresentati. E le equazioni di secondo grado generano quasi sempre due soluzioni distinte e separate. Ma due soluzioni implicano una scelta. Cioè la scelta della soluzione (tra le due possibili) che si vuole adottare.

Ehm....faccio un esempio: Date due rette non parallele, è facile immaginare una circonferenza tangente alle due rette, vero? Però non è subito intutitivo il fatto che di tali circonferenze ne esistono ben quattro!

Infatti immaginate le due rette infinite. Esse si incontrano in un punto di intersezione e generano quattro angoli che possono contenere circonferenze di un dato raggio stabiliro a priori e tangenti ai lati degli angoli. Allora visivamente è facile stabilire quale delle quattro per noi si desidera considerare. Ma il computer non può decidere per noi. Dovrebbe intuire a quale delle quattro circonferenze noi facciamo riferimento. Magari chiedendocelo esplicitamente, o accorgendosi dalla posizione del puntatore in quell'istante. Poi magari un click potrebbe confermare la circonferenza correntemente visualizzata e "la inchioda" nel disegno.
Quest'ultimo esempio è fondamentale anche per capire come si può giungere alla realizzazione di archi e linee raccordati.

Vediamo come si risolve il problema facendo il più possibile a meno delle formule, ma sempre utilizzando la base di conoscenza delle class fino ad ora create.

Lo scopo è quello di aggiungere alle class Arco e Circonferenza un ulteriore constructor che permetta di creare e disegnare la corrispondente circonferenza od arco avendo come dati iniziali solo linee e il raggio della circonferenza od arco.
Consideriamo il caso della circonferenza. Per l'arco il discorso è simile.
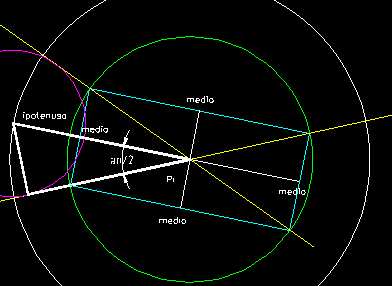
Per disegnare un circonferenza tangente a due linee bisogna considerare innanzitutto le rette di tali linee e il loro punto d'intersezione che da ora chiameremo Pi.
Ciò che non si conosce è la posizione del centro delle 4 circonferenze possibili. Ma dato che una circonferenza tangente a due linee ha due raggi ognuno perpendicolare ad una delle linee rispettivamente, possiamo affermare che ognuno dei raggi si può considerare come un cateto di un triangolo rettangolo retto nel punto di tangenza ad una linea. L'ipotenusa di tale triangolo è, invece, la distanza tra il punto Pi delle linee e il centro della Circonferenza ancora ignoto.
Per farla breve diciamo subito che a noi interessa l'ipotenusa di tale triangolo cosicchè diventa possibile stabilire la posizione del centro della circonferenza. Dai teoremi dei triangoli rettangoli si ricava che l'ipotenusa di un triangolo equivale al rapporto tra un cateto (il raggio) e il seno dell'angolo opposto al cateto (scusatemi per la piccola formula).
Il fatto è che non conosciamo l'angolo opposto. Ma guardando in figura notiamo che esso è praticamente la metà dell'angolo formato dalle due linee.
Tale angolo però ci IMPONE LA PRIMA SCELTA. Infatti essi sono due. O meglio quattro, ma a coppie uguali perchè opposti.
Allora come fa il programma a sapere qual'è l'angolo da noi desiderato? Niente da fare! Non lo sa! Bisogna considerarli entrambi (almeno per ora). Per questo è stato creato un method della class Linea che ritorna appunto i due possibili angoli formati da due linee. Questi angoli sono complementari uno dell'altro ad un angolo di 180°. Eccol il methid angolo

// angolo tra la linea in corso e un'altra linea  

  double angolo(Linea l, boolean unodeidue) {

    double ang= Math.abs(angoloXY()-l.angoloXY());

    if (unodeidue) return ang; else return Math.PI-ang;

  }

Conoscendo l'angolo (o meglio gli angoli) tra le due rette è possibile applicare la formula per il calcolo dell'ipotenusa di cui sopra. Ora non resta che posizionare il centro della circonferenza, che a questo punto ne dovrebbero essere generati già due, visto il risultato DUPLICE che il method angolo ci fornisce. Ma questo non è semplice. Una cosa è conoscere la misura di tutte le informazioni di una figura geometrica e una cosa è conoscere la sua precisa posizione e/o rotazione nell'ambito del piano XY o rispetto ad altre entitè (nel caso specifico: LE LINEE).
Un'informazione sicura è che il centro della nostra ignota circonferenza sta sicuramente posizionato sulla bisettrice del'amgolo che abbiamo calcolato. Ma le bisettrici sono due! Perchè sono due gli angoli diversi formati dalle linee.
Allora calcoliamo le bisettrici. Introduciamo un nuovo constructor per la class Linea che crea una Linea bisettrice dell'angolo formato da due linee date e il parametro unodeidue, come al solito permette di ritornare l'una o l'altra bisettrice.
Per non utilizzare formule, tale constructor trova le bisettrici rappresentando due loro qualsiasi punti ricavati da un intersezione di una ipotetica circonferenza di raggio qualsiasi (50) posizionata sul punto Pi delle due linee date. Tali punti di intersezione vengono forniti dalla class duePunti applicata ad ognuna delle due linee e a tale circonferenza. Tali punti, a coppie, rappresentano allora gli estremi di segmenti formanti un rettangolo del quale i la ti che sono le congingenti dei punti medi opposti sono le linee bisettrici che a noi interessano. Essendo quattro i punti medi di un rettangolo, sono due le bisettrici degli angoli delle due linee.

 

// linea bisettrice dell'angolo tra due linee

  Linea(Linea l1, Linea l2, boolean unodeidue) {

    P1= new Punto(l1, l2);

    Circonferenza Ci= new Circonferenza(P1, 50);

    duePunti dp1= new duePunti(l1, Ci);

    duePunti dp2= new duePunti(l2, Ci);

    Linea La=new Linea(dp1.P1, dp2.P1);

    Linea Lb=new Linea(dp1.P1, dp2.P2);

    if (unodeidue) P2=La.medio(); else P2=Lb.medio();

    m=deltaY()/deltaX();

    n=-m*P1.x + P1.y;

  }

Una volta che sono note le bisettrici, qual'è la posizione dei centri delle circonferenze?
Si ricava che il centro di ognuna delle circonferenze tangenti è posizionato proprio sulle bisettrici degli angoli menzionati, ad una distanza dal punto Pi uguale alla lunghezza dell'ipotenusa del triangolo di cui sopra. Allora se si costruisce una ulteriore circonferenza con centro nel punto Pi con raggio uguale a tale ipotenusa, si ricavano quattro intersezioni con le due linee che rappresentano appunto i quattro centri delle quattro circonferenze possibili tangenti alle due linee. /vedi figura precedente)
Ma come si fa?
Utilizzando sempre la class duePunti eseguendo l'intersezione come appena esplicato...
Conviene creare un ulteriore constructor per la class Circonferenza che crea una circonferenza tangente a due linee

// circonferenza tangente a due linee con raggio noto

// unodeidue1 regola quale dei due angoli e quindi anche bisettrice bisogna cosiderare

// unodeidue2 indica quale coppia dei due punti possibili sara' il centro

  Circonferenza(Linea L1, Linea L2, double raggio, boolean unodeidue1, boolean unodeidue2) {

    double alfa = L1.angolo(L2, unodeidue1);

    Punto pint= new Punto(L1, L2);

    Circonferenza c= new Circonferenza(pint, raggio/Math.sin(alfa/2));

    duePunti dp= new duePunti(new Linea(L1, L2, unodeidue1), c);

    if (unodeidue2) {

      centro=dp.P1;

    }

     else {

      centro=dp.P2;

    }

    this.raggio=raggio;

   }

Come potete osservare ci sono due parametri boolean unodeidue1 ed unodeidue2 che alternati tra True e False possono attivare, una alla volta, le quattro possibili circonferenze.
Riassumendo la funziene di questi due parametri si può affermare che: una volta stabilito il valore di questi due parametri la circonferenza è unica.

Naturalmente, nella stesura di un programma dinamico come un CAD tali scelte possono essere intercettate da eventi, come già spiegato, esplicitamente passati dall'operatore, o automaticamente tramite il controllo della posizione del cursore grafico e/o di vari click precedenti utili alla selezione delle linee di tangenza e quindi possibili punti di riferimento ai lati dell'anglo desiderato. Insomma questi due parametri possono essere gestiti a piacimento. Ma qui, nei nostri esempi devono essere esplicitamente espressi.

Questa è l'applet permette quanto descritto. Bisogna cliccare 4 punti che saranno gli estremi delle due linee. Il programma considera le rette corrispondenti e calcola le 4 circonferenze possibili tangenti ad entrambe le linee.

// Allora per realizare quest'applet sono necessarie queste poche righe

 

  Linea L1 = new Linea(pa, pb);

  Linea L2 = new Linea(pc, p);

  Punto Pi= new Punto(L1, L2);



  (new Circonferenza(L1, L2, 20, false, false)).disegna(Color.red, offg);

  (new Circonferenza(L1, L2, 20, false, true)).disegna(Color.magenta, offg);

  (new Circonferenza(L1, L2, 20, true, false)).disegna(Color.blue, offg);

  (new Circonferenza(L1, L2, 20, true, true)).disegna(Color.cyan, offg);

Riprendendo il discorso degli archi si deve notare che le circonferenze che si possono osservare nell'applet non sono altro che le stesse che generano gli archi di raccordo tra le due linee L1 ed L2. Sul prossimo articolo si potrà esaminare un'applet che dinamicamente ci farà scegliere tra le quattro possibilità di raccordo direttamente con il mouse. Praticamente come accade nei programmi CAD. Cioè cliccando i punti estremi delle linee e disegnare le linee. Successivamente per eseguire il raccordo si clicca sulle parti delle linee che si vogliono raccordare con un raggio stabilito magari da un valore in un TextField.

Le frequenti modifiche alle classi già presentate sono dovute al continuo miglioramento della loro struttura. E da tener presente, inoltre, che tali articoli non sono già belli e confezionati, ma vengono scritti dall'autore di volta in volta.
Basta, comunque, farsi il download dei files newGraphics.java e vectors7.java e sostituirli a quelli già downloadati in precedenza.
 


 

 

MokaByte rivista web su Java

MokaByte ricerca nuovi collaboratori
Chi volesse mettersi in contatto con noi puņ farlo scrivendo a mokainfo@mokabyte.it