Introduzione
L’evoluzione della tecnologia negli ultimi anni ha causato una crescita esponenziale della mole di dati disponibili in tutti i settori: oggi le stesse fonti generano dati in quantità di ordini di grandezza superiore rispetto a quanto potevano generare solo pochi anni fa. Si è quindi palesata la necessità di esplorare, o meglio “distillare”, queste enormi quantità di dati per cercare informazioni utili nei più svariati campi. Ed è così che parole chiave come “big data” e “data mining” sono diventate di grande attualità.
Il punto è che queste parole vogliono dire tutto e niente, perché essendo molto generiche nascondono un intero universo di metodologie di analisi applicabili a un numero altrettanto vasto di domini. Di conseguenza è necessario circoscrivere il raggio di azione a uno specifico ambito.
Analisi statistica
Un campo di applicazione che mi vede in parte coinvolto nella mia attività lavorativa è l’analisi statistica di grandi quantità di dati, in particolare raccolti dalle dogane su flussi commerciali di import ed export. Si tratta di analisi numerica di data set per lo più disponibili sotto forma di tabelle di database alla ricerca di valori “anomali”, che si distinguano, secondo uno o più criteri statistici ben definiti, dal resto della popolazione che compone quel data set. I valori anomali vengono definiti in gergo tecnico outlier, cioè “collocati/situati al di fuori” (della popolazione principale).
Gli outlier e la statistica “robusta”
La ricerca degli outlier in una popolazione è un problema statistico importante che assilla i professionisti del settore da lungo tempo [1]. Molto spesso, la presenza di outlier influenza in modo anche notevole i risultati dell’analisi e gli indicatori statistici. Quindi il problema è di natura duplice:
- Isolare gli outlier, minimizzando le possibilità di mancata individuazione (outlier non individuati) o i falsi positivi (dati contrassegnati come outlier ma che in realtà non lo sono).
- Fare in modo che il risultato dell’analisi e le relative conclusioni o indicatori non siano influenzati in modo apprezzabile dalla presenza degli stessi outlier.
Gli outlier trovati possono, a seconda dei casi e del contesto, costituire “segnali” particolarmente interessanti per l’indagine in corso — ad esempio frodi commerciali — oppure rivelare problemi nella qualità e/o nella gestione dei dati, ad esempio un semplice errore nella dichiarazione doganale.
In questo secondo caso, in generale essi devono essere scartati perché influenzerebbero negativamente la qualità del risultato dell’indagine. Le metodologie statistiche che rispondono agli obiettivi e alle esigenze di cui sopra sono note con il nome di metodi robusti [2].
Metodi robusti: alcuni esempi
Per spiegare il concetto ricorriamo ad alcuni esempi che ci consentano di capire, in modo semplificato ma tutto sommato corretto, alcuni termini statistici.
Mediana come stimatore robusto
Per prima cosa consideriamo l’altezza in metri di un piccolo gruppo di ragazzi: 1.65, 1.67, 1.68, 1.70, 1.72, 1.77, 19.5. L’ultimo è un outlier, e chiaramente si tratta di un dato errato: con ogni probabilità un errore di posizionamento del punto decimale. Ad ogni modo, a prescindere dalla motivazione dell’errore, se calcolo la media delle altezze trovo 4.24, mentre calcolando la media lasciando fuori l’outlier ottengo 1.70, risultato intuitivamente migliore.
Se però usiamo la mediana, calcolata prendendo il valore intermedio:
1.65, 1.67, 1.68, 1.70, 1.72, 1.77, 19.5
troviamo 1.70, risultato indentico al valore della media calcolata non considerando l’outlier. Si vede come la media sia molto più sensibile della mediana alla presenza degli outlier. Si dice allora che la mediana è uno stimatore robusto, mentre la media non lo è.
Regressione lineare
Consideriamo ora un concetto un po’ più complesso. Dobbiamo realizzare una regressione lineare, una tecnica usata in molte scienze applicate (chimica, geologia, biologia, fisica, ingegneria, medicina, scienze sociali, etc.) per trovare una relazione di tipo lineare tra una o più variabili cosiddette indipendenti e una variabile dipendente; il caso più semplice è quello con una sola variabile dipendente, che può essere agevolmente rappresentato su un grafico bidimensionale.
I punti che compongono il grafico sono tipicamente presi da una popolazione reale di cui vogliamo studiare il comportamento. Ad esempio, vogliamo vedere se in un campione di impiegati di una multinazionale esista una qualche relazione tra il numero di anni di esperienza lavorativa e lo stipendio.
Se disponiamo i dati in nostro possesso in un grafico, avente sulle asse delle ascisse (“X”) gli anni di esperienza e sulle ordinate (“Y”) lo stipendio lordo, otteniamo un grafico come quello di figura 1.
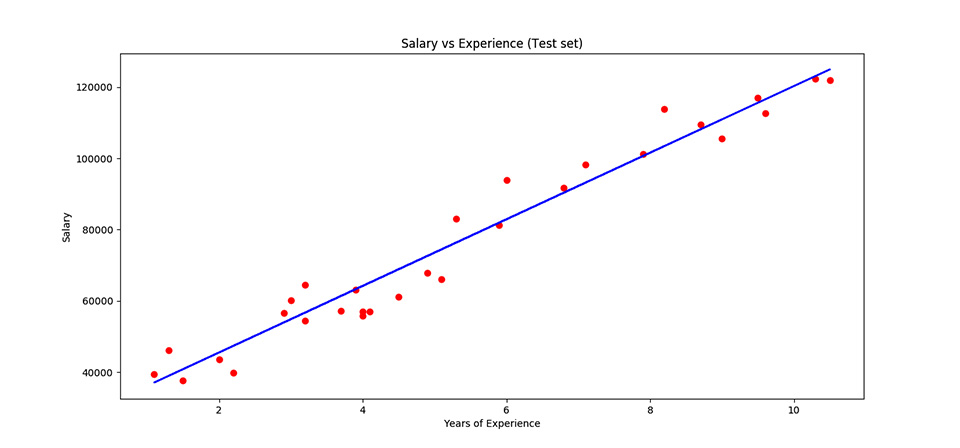
In questo caso si vede come i dati, pur non essendo posti perfettamente lungo una linea, mostrano una disposizione che suggerisce l’esistenza di una relazione abbastanza chiara tra gli anni di esperienza e lo stipendio. La linea di regressione è la retta blu.
La “bontà della disposizione dei punti su una retta” è descritta da un parametro chiamato R2, detto coefficiente di determinazione e indica la bontà della curva di regressione, nel nostro caso una retta, cioè quanto bene (o male) questa retta rappresenti l’effettiva relazione tra le due variabili espressa dai punti.
Il valore R2 varia tra 0, che indica un insieme di punti sparsi e quindi completamente scorrelati fra loro, e 1, che si ottiene invece quando i punti sono tutti posti perfettamente lungo una retta. La figura 2 illustra bene il concetto del valore di R2.
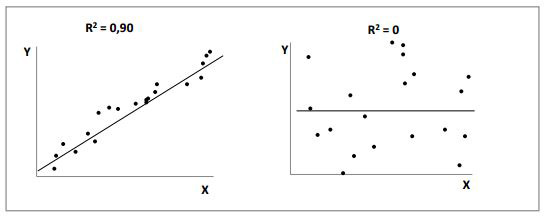
I punti del grafico a sinistra sono chiaramente legati fra di loro, mentre quelli del grafico di destra sembrano essere disposti in maniera del tutto casuale.
La regressione lineare funziona bene se i dati hanno un “buon” R2 e non mostrano particolari anomalie. La situazione può cambiare radicalmente quando i dati siano affetti da uno o più outlier di posizione estrema rispetto alla maggioranza della popolazione, il che può portare a errori anche gravi nel risultato.
Forward-search
Consideriamo ora un altro esempio. Abbiamo effettuato un esperimento registrando la temperatura di ebollizione dell’acqua (in gradi Fahrenheit) a seconda della pressione atmosferica (in pollici di mercurio, scala logaritmica). Con le nostre osservazioni costruiamo il grafico rappresentato in figura 3.
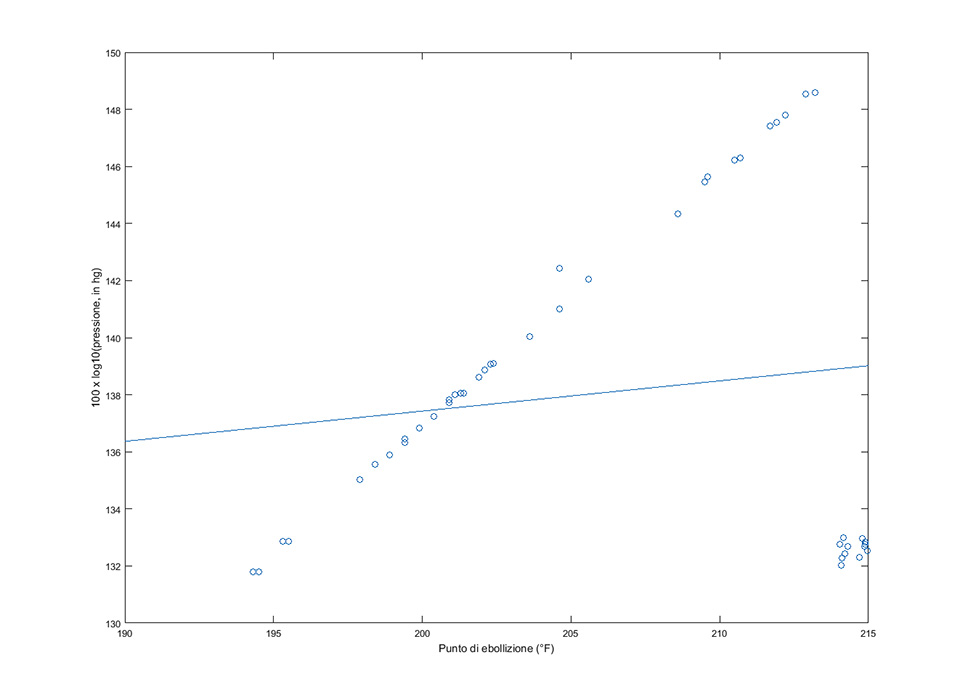
Il grafico mostra il grosso dei valori disposti lungo una linea (insieme di punti disposti quasi sulla diagonale), più un gruppo in basso a destra staccato dalla popolazione principale. La retta di regressione (azzurra continua) ottenuta dall’intero insieme di dati ha un’inclinazione molto inferiore a ciò che il grafico suggerisce, ed è chiaramente errata.
Intuitivamente, dobbiamo trovare un modo di calcolare la retta di regressione escludendo il gruppo che si trova in basso a destra. Si pone ora il problema di quale criterio usare per operare questa distinzione. Quale che sia il criterio, esso deve essere naturalmente supportato da solide basi teoriche.
In nostro aiuto viene l’utilizzo di un metodo robusto. La letteratura ne offre diversi: scegliamo la cosiddetta forward-search [3] [4] [5], applicando ai nostri dati una funzione opportuna del pacchetto FSDA [6] di MATLAB, descritto più avanti. Il risultato è mostrato in figura 4.
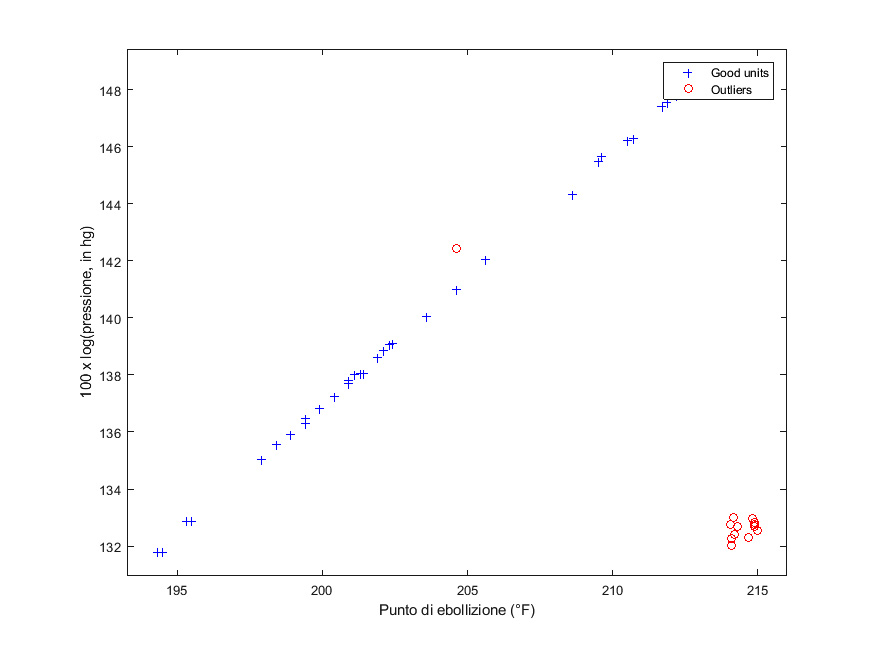
Lo stesso insieme di dati, analizzato con la forward search, è stato stavolta suddiviso in due gruppi ben distinti: la popolazione “principale” (crocette blu) e gli outlier (pallini rossi). La retta di regressione è stata calcolata lasciando fuori gli outlier: come si può vedere, essa è in ottimo accordo con la disposizione della popolazione principale.
Abbiamo esaminato un caso abbastanza semplice, ma nella pratica gli outlier in una popolazione possono essere presenti in quantità e qualità tali da costituire una notevole sfida per matematici e statistici. Il tutto si complica nel caso di popolazioni multivariate, per le quali non è possibile ricorrere all’ausilio visivo e intuitivo dei grafici bidimensionali.
Il toolbox FSDA
Diversi software dedicati al calcolo statistico, matematico e finanziario (MATLAB, R, SAS, etc.) offrono oggi una varietà di metodi e pacchetti per la ricerca e l’eliminazione di outlier. In questo e nel prossimo articolo dedicheremo un po’ di paragrafi al toolbox FSDA (Flexible Statistical Data Analysis) [6] sviluppato in MATLAB da un team di ricercatori e programmatori provenienti dal mondo accademico e da istituzioni di ricerca internazionali.
FSDA è completamente gratuito e liberamente scaricabile e offre un’ampia gamma di funzionalità, come ad esempio:
- funzioni per la regressione robusta, come quella usata per analizzare il data set precedente;
- funzioni per l’analisi robusta multivariata;
- funzioni per il clustering robusto multivariato (tecnica di analisi avente il fine di selezionare e individuare gruppi di elementi omogenei in un insieme di dati);
- capacità grafiche avanzate per l’analisi interattiva dei dati;
- documentazione molto dettagliata e corredata di numerosi esempi [7].
L’esempio della funzione FSR()
In particolare, per analizzare il data set del punto di ebollizione dell’acqua, è stata utilizzata la funzione che effettua una regressione robusta tramite la forward search, FSR().
load('data.txt');
y=data(:,2);
X=data(:,1);
plot(X,y,'o');
xlabel('Punto di ebollizione (°F)')
ylabel('100 x log(pressione, in hg)')
FSR(y,X)
xlabel('Punto di ebollizione (°F))
ylabel('100 x log(pressione, in hg)')
Il progetto FSDA viene portato avanti ormai da molti anni. Da qualche tempo collaboro con il team di sviluppo, soprattutto per gli aspetti di qualità del software. Anche se siamo di fronte a software non scritto in un linguaggio orientato agli oggetti (MATLAB ha invero una sua sintassi per l’OO, non usata in FSDA per problemi di retrocompatibilità), il testing automatico si è rivelato assai utile per migliorare la qualità del software.
Conclusioni
In questo articolo abbiamo descritto — solo sfiorato, in realtà — le problematiche che gli analisti e gli specialisti di data mining si trovano spesso ad affrontare nell’analisi di grandi quantità di dati numerici, cercando di separare i dati “buoni” da quelli anomali e usando solo i primi come base fondante delle loro analisi.
Agli analisti spetta anche il compito di formulare ipotesi sull’origine delle anomalie, ad esempio distinguendo tra dati effettivamente anomali — dunque parte integrante del fenomeno analizzato, e spesso meritevoli di attenzione — da altre fonti di disturbo, come ad esempio problemi di qualità dei dati (errori nella raccolta, etc.).
Nel prossimo articolo descriveremo più in dettaglio un caso concreto di applicazione di testing automatico al toolbox FSDA, implementato con l’obiettivo di migliorare la qualità del software in un progetto già avviato e maturo, minimizzando però il carico di lavoro richiesto.


