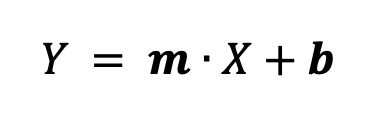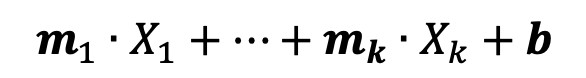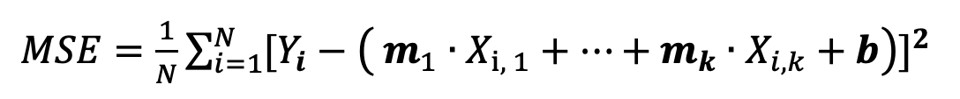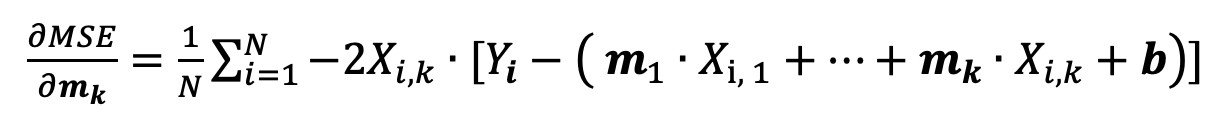Algoritmi quotidiani…
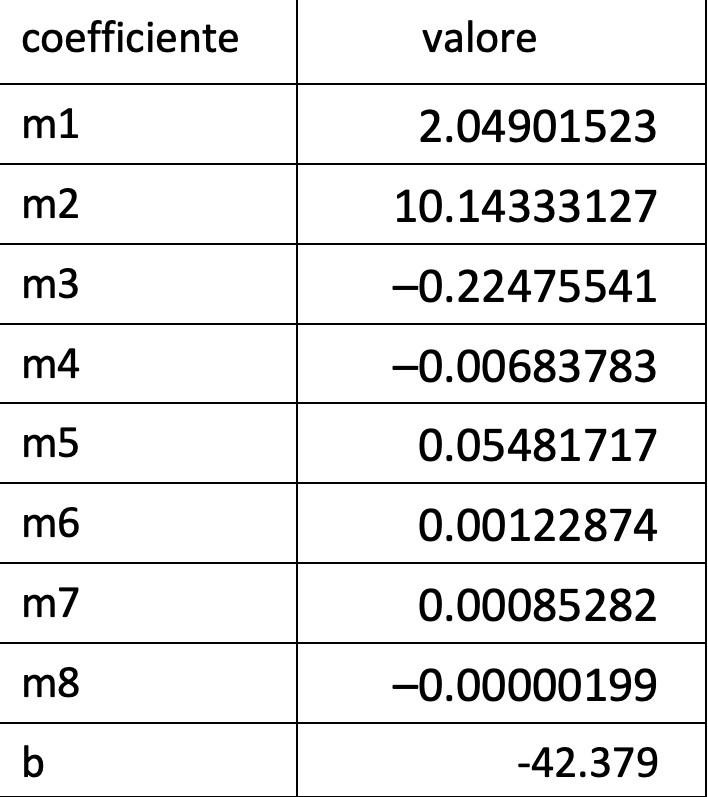
Più o meno tutti abbiamo sul telefono una app che fornisce le previsioni del tempo. E molte app che forniscono le previsioni del tempo indicano anche la cosiddetta “temperatura percepita”, vale a dire la sensazione di fastidio causata da condizioni di caldo afoso. In meteorologia esiste un metodo acclarato per il calcolo della “temperatura percepita” che si basa proprio su umidità e temperatura.
Tale metodo consiste nel calcolo di una formula con coefficienti alquanto innaturali:
Nella formula, H rappresenta l’umidità e T la temperatura misurata.
Questa formula non lineare — perché compaiono i quadrati di T e di H — è il risultato di un procedimento noto come regressione (statistica). Si parte dai dati osservati sul campo e si cerca una formula che “aderisca” bene.
Il procedimento, in linea di principio, si compone di tre parti:
si ipotizza che una certa formula vada vagamente bene,per esempio una formula lineare, cioè una retta:
si decide come calcolare l’errore fra la predizione che fa la nostra formula e il valore che abbiamo effettivamente registrato sul campo;
infine si tenta di ridurre il più possibile l’errore.
Regressione lineare
Partiamo col dire che dalla formula iniziale che scegliamo dipende quasi tutto. Nel caso più semplice, chiamato appunto regressione lineare, supponiamo che vada bene una linea retta.
Partiamo dal caso semplice (e irrealistico) di un input fatto da una sola variabile. Lo spazio di riferimento è R2 e abbiamo detto che cerchiamo una retta che approssimi i dati, che quindi avrà questa forma:
In più dimensioni, vale a dire se c’è più di un input (come nel caso sopra con temperatura ed umidità),
il processo di learning (o training) servirà a trovare i coefficienti ideali per gli m e b.
Tali valori ideali dei coefficienti risulteranno dalla minimizzazione di una funzione matematica che descrive l’errore (o la distanza) tra il valore calcolato dalla nostra approssimazione e il valore misurato sul campo. Il valore calcolato dalla nostra approssimazione corrisponde a:
dove le X sono gli input che abbiamo.
Supervised learning
La regressione lineare, infatti, è un meta algoritmo — nel senso che è descritto a grandi linee ma si può implementare in molti modi diversi — di supervised learning, che parte da valori noti di input e valori noti di output e trova la strada migliore per arrivarci.
Esistono fondamentalmente due approcci per minimizzare l’errore: analitico e machine learning. L’approccio analitico consiste nel considerare il dataset alla stregua di una matrice e di operarvi con procedure di calcolo matriciale: fattibile, ma poco scalabile quando le cose si complicano.
L’approccio machine learning, invece, è di tipo iterativo e funziona così: inizialmente assegna valori casuali ai coefficienti e calcola l’errore tra valore predetto e valore vero. Se l’errore è troppo grande, cambiano i coefficienti di iterazione in iterazione fino al raggiungimento di una soglia accettabile.
La funzione d’errore
Il ruolo chiave nella regressione lineare lo gioca dunque la funzione d’errore, che dovrà essere resa più piccola possibile; andrà cioè minimizzata. Di essa andrà trovata una definizione analitica e un metodo di minimizzazione. La formula analitica dice in che modo verrà calcolato l’errore; il metodo di minimizzazione dice in che modo verranno modificati i coefficienti di volta in volta per ridurlo.
Una prima formulazione della funzione d’errore è la semplice somma degli errori riscontrati su tutto il dataset. Però in questo modo errori positivi e negativi si annullerebbero rendendo inefficace il metodo. Passare al valore assoluto della differenza è una strategia migliore sebbene non perfetta. La funzione valore assoluto, infatti, non è derivabile in tutti i punti del dominio. Già, ci servono le derivate. Alla fine, l’opzione migliore è rappresentata dallo scarto quadratico medio (MSE):
La funzione è derivabile ovunque e per costruzione — il quadrato dei valori — dà più rilevanza agli errori grandi e meno a quelli piccoli. Nella formula, N è la dimensione del dataset e Yi il valore atteso per l’i.ma riga.
Trovare i valori ideali dei coefficienti richiede la minimizzazione della funzione MSE. Abbiamo una funzione multi-variabile e la matematica ci dice che la tecnica chiave per la minimizzazione di tali funzioni è la discesa del gradiente.
Il gradiente è un vettore contenente i valori di tutte le derivate parziali rispetto alle varie variabili della funzione in un dato punto del dataset. Qui chiariamo un punto chiave: durante il training le variabili non sono le X — quelle rappresentano i valori di input —, bensì gli m e b. Ad esempio, ecco la derivata parziale rispetto a mk:
Una volta “addestrato” l’algoritmo, e messolo in produzione, invece i coefficienti rimarranno fissi e di volta in volta, per predire il risultato, si dovranno inserire nella formula solo gli input X.
Tornando al training, il nuovo i.mo coefficiente risulta dall’applicazione della seguente regola:
Coefcurrent – alpha * gradienti
Il valore corrente del coefficiente i.mo viene decrementato del valore dell’i.ma componente del gradiente moltiplicato per un fattore alpha, noto come learning rate.
Questo ha senso perché, in generale, il gradiente indica la direzione di massima crescita della funzione. Avendo qui un obiettivo di minimizzazione, è necessario applicare un fattore negativo, cioè andare nella direzione opposta.
Iperparametri
È interessante notare che alpha indica quanto si vuole andare nella direzione opposta a quella indicata dal gradiente. Tipicamente alpha assume valori molto piccoli tra 0 e 1.
Nel caso della regressione lineare, ci sono (altri) due iperparametri interessanti, perché vengono utilizzati per far terminare l’algoritmo. Uno è la soglia di errore che definisce quanto accettabile possa essere un errore. In altre parole, data la soglia, se si ottiene un errore minore, si termina l’algoritmo.
Un altro è la soglia di miglioramento, vale a dire che quando il miglioramento riscontrato tra una iterazione e l’altra è inferiore alla soglia, allora è lecito concludere che non esistono più grandi margini di miglioramento e dunque si può terminare.
Statistica vs Machine Learning
In generale, sia in statistica che in machine learning, il compito della regressione — in questo caso lineare — è sempre lo stesso: approssimare con una formula i valori disponibili.
La statistica però effettua un’analisi statica e post mortem dei dati disponibili, mentre il machine learning usa gli stessi dati per individuare una tendenza di comportamento e guarda al passato per predire un ragionevole futuro. Mentre la regressione statistica, per definizione, deve aderire ai dati passati e spiegarli, in machine learning il focus è sulla previsione dei futuri valori.
Conclusioni
La vivisezione di un algoritmo di machine learning non porta di per sé vantaggi concreti nella costruzione di soluzioni di intelligenza artificiale. Al tempo stesso, una conoscenza anche solo superficiale della matematica che gira dietro gli algoritmi è utile per non cedere al senso di “magia nera” che pervade spesso l’intera area dell’intelligenza artificiale. La regressione lineare è il caso più semplice di algoritmo; ne vedremo altri, più sofisticati, nelle prossime puntate.
I spent 21 years (so far) trying to make sense of the crazy amount of unsolicited input I was asynchronously receiving, whether literature, art, mathematics, computer science or machine learning.
In 2012, when I was 14 I began my software development journey the hard way with some iOS development, then I took the smoother route up to C# and ASP.NET.
I founded a (small) company called Youbiquitous to remind every moment of my life that I can be everywhere and speak to anybody about anything. At some later point, the deep love for mathematics reemerged and led to take the plunge in financial investments and machine learning.
I have a dream too: developing the super-theory of intelligence which would mathematically explain why deep learning works.