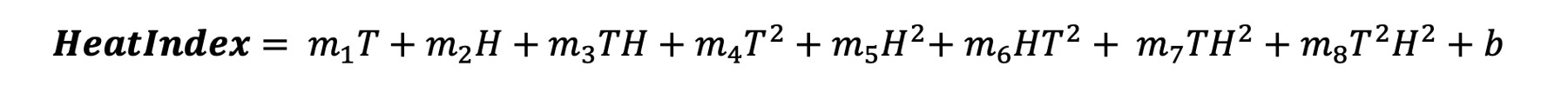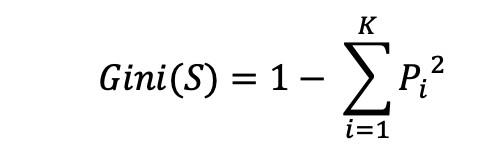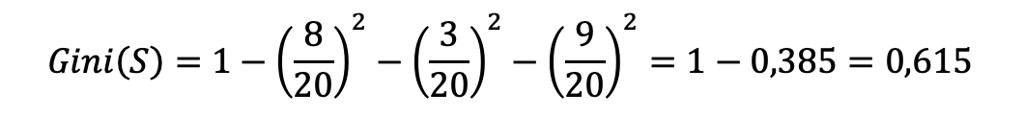Oltre la regressione lineare

Nello scorso articolo abbiamo lavorato sulla regressione lineare (e multi–lineare) e abbiamo visto come produrre una previsione a partire dai dati storici a disposizione. Lì il trucco era scegliere la formula di una retta in grado in grado di minimizzare l’errore nel dato predetto.

Peccato che tale approccio funzioni (bene) solo se abbiamo relazioni lineari, cioè quasi mai nel mondo reale. Cosa si può fare altrimenti? Si può procedere in due modi:

• si aggiungono dati al dataset;
• si tentano approcci diversi.

Per illustrare il primo scenario riprendiamo l’esempio del calcolo della temperatura percepita discusso nell’articolo precedente. La formula dipende da due variabili: temperatura e umidità.

Come si vede, però, nella formula compaiono i quadrati delle temperature e ciò rende la formula non lineare. Potremmo dunque semplicemente aggiungere una colonna al dataset che contenga il quadrato delle temperature e trattarla esattamente come se fosse una variabile lineare. Questo approccio in realtà funziona solo finché sappiamo che tipo di relazione aspettarci, altrimenti non possiamo certo metterci ad aggiungere una colonna per ogni relazione non-lineare che ci viene in mente.

In alternativa ci si deve industriare e ricercare approcci diversi, con difficoltà crescenti. Il primo tentativo che vale la pena fare è con gli alberi di classificazione e regressione.

Gli alberi

Gli alberi sono strutture dati composti da nodi e da collegamenti fra nodi, detti archi; hanno una radice e ogni altro nodo esclusa la radice ha uno ed un solo “genitore”; due nodi con genitori diversi non possono essere collegati e due nodi con lo stesso genitore sono collegati solo attraverso il genitore; i nodi “finali”, cioè senza figli, si chiamano foglie. Più difficile a dirsi che non a capirsi con una figura.

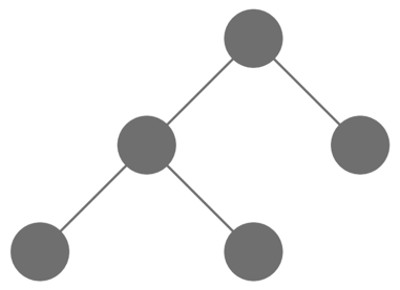
Un algoritmo tree–based è un algoritmo che usa l’albero e la sua struttura per prendere decisioni, come fosse un diagramma di flusso. Anche qui, più difficile a dirsi che a vedersi.

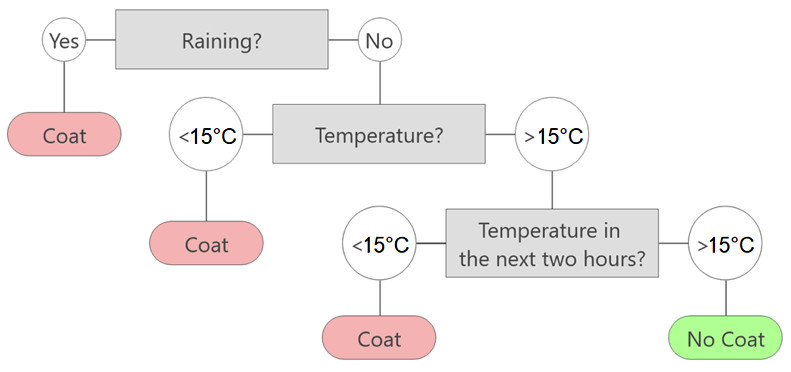
Quindi se qualcuno ci desse un albero già pronto, potremmo prendere decisioni a partire da quello semplicemente seguendo le domande che vengono poste ad ogni nodo e scegliendo la risposta adatta al nostro caso. Normalmente si usano alberi binari per semplificare le cose, vale a dire che si pone la domanda in modo che la risposta possa essere solo “sì” o “no”.

Alberi di classificazione e di regressione

Un albero può fare sia classificazione che regressione. Fare classificazione significa attribuire una categoria — fra un numero complessivo e finito di categorie iniziali — al dato iniziale. È una cosa che la regressione lineare non poteva fare, giacché la regressione non predice una categoria ma un numero reale continuo.

Per rendere più chiara la differenza, classificando il colore di un oggetto posso avere come risultato solo i colori stessi — rosso, blu, verde… o equivalentemente dei numeri interi: 1,2,3… — e non qualcosa di intermedio. Tentando di predire il prezzo di un taxi invece posso ottenere un numero “continuo”: per esempio posso ottenere 12,25 euro o 103,65 euro.

Per semplicità considereremo un albero di classificazione.

Come costruire un albero di classificazione

Nel caso del machine learning, non abbiamo qualcuno che ci dia un albero pronto con le domande già fatte— altrimenti sarebbe un cosiddetto sistema esperto — ma dobbiamo capire come costruire un albero adatto per prevedere i dati futuri a partire dal dataset che abbiamo.

L’obiettivo è costruire un albero che faccia le domande giuste per capire come classificarci. Ogni domanda esegue uno split del dataset, in questo senso: le domande servono a dividere il dataset in molte regioni diverse e attribuire ad ogni regione una classificazione. In particolare la classificazione scelta per ogni regione è la classificazione più comune in quell’area. Ogni domanda serve a “partizionare” ancora di più il dataset, in base alle caratteristiche dei dati. Chiaramente le domande vengono fatte proprio per discriminare i dati in base ai valori che assumono certe “colonne”.

Per esempio, prendendo l’albero di figura 2 (in cui c’è da classificare “Cappotto sì / Cappotto no”) e domandando “Piove?”, stiamo dividendo il dataset in due aree: una è costituita dai dati per cui effettivamente pioveva, l’altra dai dati in cui non pioveva. Cioè discriminiamo in base alla colonna “Pioggia” presente fra le informazioni sul dato, cioè nel dataset.

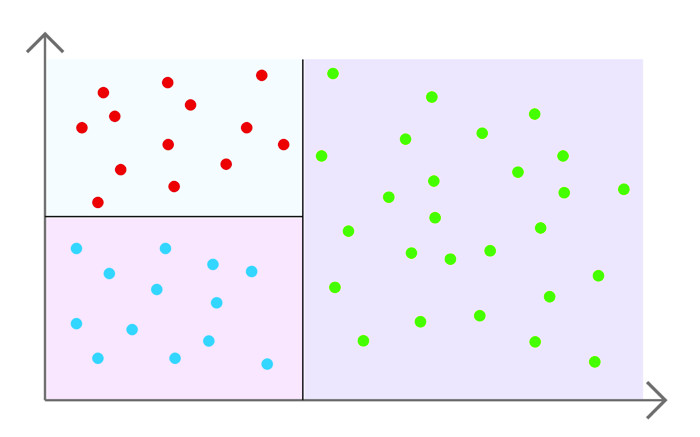
Immaginando di non fare altre domande e dover fermare subito il nostro albero, la prima area (quella in cui pioveva) verrà classificata considerando tutti i dati che ci sono lì e scegliendo la classificazione più comune per quei dati.

“Addestrare” l’albero

Non dimentichiamo infatti che stiamo “addestrando” (costruendo) il nostro albero e quindi abbiamo a disposizione un dataset con i dati che contengono già le risposte corrette. Nello specifico probabilmente in quell’area la classificazione più comune sarà “Cappotto sì”. Quindi scriveremo nella foglia di sinistra “Cappotto sì”, mentre in quella di destra prenderemo la classificazione più comune per l’area costituita dai dati in cui non piove (che sarà probabilmente “Cappotto no”).

Ricapitolando, ogni domanda serve a dividere il dataset in partizioni distinte e poi le foglie danno il responso finale (vale a dire la categoria da predire), in base a quale sia la classificazione più comune per tutti i dati che cadono in quella specifica area.

Quando è finito l’addestramento e si presenta un dato nuovo — cioè senza che qualcuno lo abbia già classificato “a mano” — gli si fa seguire l’albero con le domande e le rispettive risposte. Quando ci si ferma si sarà arrivati a una foglia. Sulla foglia sarà scritta la categoria predetta, decisa durante l’addestramento.

Omogeneità e funzione di errore

La domanda rimane: come si costruisce esattamente un buon albero di classificazione?

Abbiamo detto che vogliamo dividere il dataset in varie regioni e prendere la classificazione più comune per quella regione. Il nostro obiettivo però deve essere anche quello di costruire regioni omogenee. La giustificazione di questo fatto è chiara: se in una regione ci sono punti con tante classificazioni diverse, allora scegliere a maggioranza quella più frequente è poco più che indovinare. Se invece la regione è omogenea — cioè quasi tutti i dati hanno la stessa classificazione — vorrà dire che quella regione è stata costruita bene, cioè sono state fatte le domande giuste.

Siccome vogliamo regioni quanto più omogenee possibili, ci riportiamo a quanto visto nel primo articolo: trovare una funzione di errore e minimizzarla. Infatti dovremo scegliere le domande da fare per minimizzare le “impurità”. Per farlo serve una definizione matematica di omogeneità (e impurità), e ne esistono due prevalenti: Gini-Index ed Entropia.

Il Gini-Index è definito così:

In questa formula, S è il dataset, K sono le categorie possibili da assegnare a ciascun dato e Pi è la frequenza degli elementi della categoria i-esima nel dataset. Esempio: se c’è un dataset con 20 film di cui 8 classificati con 1 stella, 3 con 2 stelle, 9 con 4 stelle allora:

Il Gini–Index — che prende il nome dallo statistico italiano Corrado Gini (1884-1965) — misura la probabilità di classificare male i dati. Quindi più è basso, meglio è. Infatti, se immaginassimo un gruppo totalmente omogeneo — cioè, nel nostro esempio, 20 film classificati tutti e 20 con 3 stelle — il Gini-Index sarebbe 0.

Il principio di costruzione dell’albero

Il principio di costruzione dell’albero è molto semplice: si parte dovendo scegliere la radice, poi si ripete lo stesso procedimento per gli altri nodi.

1. Calcoliamo il Gini-Index per il dataset allo stato attuale dell’albero.
2. Per ogni feature (cioè colonna del dataset, escludendo la colonna che contiene la classificazione effettiva):
   1. calcoliamo il Gini-Index per ogni possibile split sul valore della feature in esame;
   2. calcoliamo il gain (cioè di quanto migliora il Gini-Index scegliendo questa feature per fare lo split).
3. Scegliamo la feature e lo split con il maggiore gain.
4. Ripetiamo fino a che non abbiamo raggiunto una certa impurità sufficientemente bassa o una certa altezza dell’albero.
5. Il valore predetto è la classe più frequente nella foglia terminale raggiunta.

Tenendo presente che trovare un albero ottimale è un problema NP, bisognerà scendere a compromessi per avere una soluzione che vada “abbastanza bene”; da qui il senso del punto 4 dell’algoritmo sopra espresso. Più l’albero è profondo, più si rischia l’over fitting. La massima profondità dell’albero dipende da quanto accurata deve essere la previsione e da quanto deve essere veloce.

Conclusioni

Gli algoritmi di machine learning tree–based sono utilissimi quando si ha a che fare con problemi non lineari, perché non si tenta più di indovinare una formula, ma si divide il dataset in regioni simili, che quindi incorporano automaticamente tutta la non linearità delle relazioni in gioco.

Inoltre sono molto interpretabili e comprensibili, vale a dire che è facile comprendere il perché di una certa classificazione. Questo sembra essere un punto irrilevante, ma non lo è: avere a che fare con una scatola nera incomprensibile, soprattutto in contesti delicati, può essere pericoloso.

Infine, si possono spesso combinare fra loro vari alberi per produrre classificazioni sempre più accurate: si tratta delle cosiddette random forest.